ポアソン分布と指数分布

数多くの部品のどれかが故障する、スーパーのレジに客がくるというような場合を考えます。１日、１分間などの単位時間にそれらの事象が起こる回数は、平均的にはわかっていますが、個々の故障や客がいつくるかはわかりません。たとえば、客の平均到着率が１時間に１０人だと統計的にはわかっていても、１５人の場合もあるし、５人の場合もあります。

ここで、次の仮定をします。この３つの仮定を満足するということは、客の来かたは「でたらめ」だということです。それをランダムだといいます。

独立性

ある事象が次に起こる確率は、これまでの経過に関係しない。
先に大勢来たから次はあまり来ないだろうということはないとします。

定常性

ある事象が起こる確率は、対象とする期間中は一定である。
スーパーなどでは、時間帯により客の数は異なりますが、検討対象とする時間の間では、変化しないと仮定します。

稀少性

微小時間内に、ある事象が２回以上起こることはない。

１時間という長さでは２人以上来るでしょうが、１分間、１秒間という微小時間でとらえれば、その間に２人以上来ることはないと仮定します。

ポアソン分布

単位時間中にある事象が発生する平均回数をλとするとき、単位時間中にその事象がｘ回発生する確率密度Ｐ(x)は、ポアソン分布に従う。
　　　　　　　λ^x
　　　Ｐ(x)＝──ｅ^－λ　　　ｅは自然対数の底＝２.７１８
　　　　　　　x！

例題

ある店では、１時間に平均５人の客が来る。客の来かたはランダムだとするとき、１時間に３人の客が来る確率を求めよ。

解答

λ＝５［人／時間］、ｘ＝３［人／時間］を公式に代入する。
　　　　λ^x　　　　　　５³　　　　　　１２５
Ｐ(x)＝──ｅ^－λ＝──────ｅ^－５＝───×０.００６７３８
　　　　x！　　　　３×２×１　　　　　６
　　 ＝０.１４０４

解説

この公式の証明は、数学的に高度なので省略します。また、計算も面倒ですので、数表や表計算ソフトを用いることにします。
なお、ポアソン分布は、平均＝λ、分散＝λになります。平均＝分散の関係があるのが特徴です。

Ｅｘｃｅｌの関数

ポアソン分布の確率密度Ｐ(x)と累積確率∑Ｐ(x)を求める。
　　　POISSON(ｘ,λ,FALSE/TRUE)　　　FALSE：Ｐ(x)、TRUE：∑Ｐ(x)
　例：POISSON(3,5,FALSE)＝0.1404
　　　POISSON(3,5,TRUE)＝0.2650

ポアソン分布のグラフ

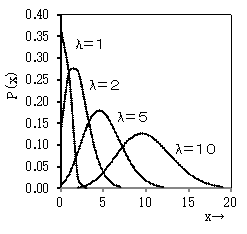発生頻度の平均λを変えて、発生頻度ｘとその確率Ｐ(x) のグラフを描くと右図のようになります。ｘ＝λのときに最大になりますが、λが小さいときは左寄りの山になり、λが大きくなると左右対称になり正規分布のようになります。
これは次のように解釈できます。１時間を単位にとれば、来客数は平均１０人程度で、毎時間の来客数は１０人のまわりに正規分布すると考えてもよいでしょう。ところが、１分単位にすれば、客は来るか来ないかのどちらかになり、２人以上来る確率は非常に低くなります、λ＝１がそのような状況を示しているのだといえます。
このように、ある事象をとらえるには時間の単位が重要であり、それによって正規分布として考えるかポアソン分布として考えるのが適切かが変わってくるのです。

ポアソン分布の計算プログラム

指数分布

単位時間中にある事象が発生する平均回数をλとするとき、その事象の発生間隔がｔ単位時間である確率密度Ｐ(ｒ)は、指数分布に従う。
　　　Ｐ(t)＝λｅ^－λｔ
０～ｔの累積確率は次式になる。
　　　Ｐ(≦ｔ)＝１－ｅ^－λｔ

例題

ある店では、１時間に平均５人の客が来る（客の平均到着間隔は１２分である）。客の来かたはランダムだとするとき、客が来てから次の客が来るまでの間隔が１５分以内である確率を求めよ。

解答

λ＝５［人／時間］、ｔ＝０.２５［時間］を公式に代入する。
Ｐ(≦0.25)＝＝１－ｅ^-1.25＝１－０.２８６５＝０.７１３５

指数分布とポアソン分布の関係

ポアソン分布は、単位時間内に事象の起こる確率であり、指数分布は事象の起こる間隔です。同じ事象を逆の視点で見ていることになります。それで、指数分布の平均は１／λになります（分散は１／λではなく、１／λ²になり、平均＝標準偏差になります）。

連続変数と確率密度

Ｐ(0.25)＝５ｅ^－5*0.25＝1.4325 を、「客の到着間隔が１５分である確率」だとしてはいけません。確率は１以上になりませんし、「１５分ピッタリ」に次の客がくる確率は０になると考えられます。高度な数学の概念が必要なので説明は省略しますが、この1.4325は確率密度で確率ではないのです。
「客の到着間隔が１５分である確率」を知りたいのであれば、累積確率（これは確率です）Ｐ（≦ｔ) を用いて、Ｐ(≦15.5分)－Ｐ(≦14.5分) のようにする必要があります。
ポアソン分布のときは、確率密度＝確率のような説明をしましたが、この場合は客の人数（整数で連続量ではない）ので、このような問題にはならなかったのです。

Ｅｘｃｅｌ関数

指数分布で、ｔを与えて確率密度Ｐ(t)と累積確率Ｐ(≦t)を求める。
　　　EXPONDIST(ｔ,λ,FALSE/TRUE)　　　FALSE：Ｐ(t)、TRUE：Ｐ(≦t)
　例：EXPONDIST(0.25,5,FALSE)＝1.4325
　　　EXPONDIST(0.25,5,TRUE)＝0.7135

指数分布の計算プログラム

待ち行列の理論

スーパーでのレジを考えます。客の到着は平均λ［人／時間］のポアソン分布に従い、レジでの所要時間は平均ｔ［時間／人］の指数分布に従うとします（すなわち、客の到着もレジでの時間もランダムだということです）。
このとき、客が到着したときレジが開いている確率、行列の平均長さ、待っている時間などに関する理論を「待ち行列の理論」といい、ＯＲ（オペレーションズ・リサーチ）のポピュラーな分野になっています。
→参照「待ち行列の概要」（que-intro）