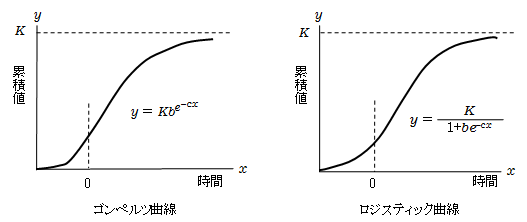
生物の個体数、新製品の販売数、プログラムのバグ発見数など、当初は少なく、中途で大きくなり、その後また少なくなるような現象は多くあります。それを時間の推移と累積量をグラフにすると、下図のようになります。これを成長曲線といいます。
基本的な形式にシグモイド関数があります。
代表的な成長曲線に、ロジスティック曲線とゴンペルツ曲線があります。両者とも、似たようなS字型の曲線で、時間xが経つにつれ、増加が止まり一定値Kに近づきます。
その違いは、増加を規定する考え方、すなわち dy/dx にあります。
ロジスティック曲線 dy/dx = Ay (K-y)
ゴンペルツ曲線 dy/dx = Ay e-cx
両者とも現在の個体数に比例して増加しますが、減少要因がロジスティック曲線では飽和点kのの差であるのに対して、ゴンペルツ曲線では時間による低下であることです。
シグモイド関数
シグモイド関数は、 y = s(x) = 1/(1+e-ax) で定義されます。(学術的には ς (シグマ) が用いられますが、活字の都合でここでは s で代用します) y を普及率、xを時間と考えるとわかりやすいです。 なお、a=1 のとき y = s(x) = 1/(1+e-x) を標準シグモイド関数といいます。 そのグラフは、次のような曲線になります。 最初はゆっくりと増加する 次第に増加速度が上昇する しかし、x = 0 を超えると増加速度は減少する そして、一定のレベル(1)に収束する という、成長曲線になっています。
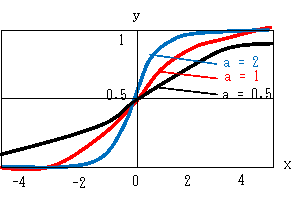
点 (0, 0,5) が対称点になり、x = -∞ で0、x = ∞ で1 になります。 aは傾きを示します。a→大 で 傾きが急になります。 (標準シグモイド関数のx軸を 1/a に狭めた曲線です) a →∞ では、x < 0 で0,x = 0 で 1/2, x > 0 で1の階段状になります。 これは、階段状関数を微分可能な関数にするときに有効で、AI分野で利用されています
微分
dy/dx = a * y * (1-y) すなわち、普及率の増加は、現在の普及率と未普及率の積に比例するといえます。
tanh 表現
y = (1 + tanh(ax/2))/2
ロジスティック曲線(Logistic curve)
生物は親から生まれるので、生物の個体数の増加率 dy/dx は直前の個体数yに比例すると考えられます。 しかし、現実には無限に増大することはありません。その限界値Kに近づくと増加率は低下するはずです。 この関係により、次の式が成立します。 dy/dx = Ay(k-y) =(c/k)y(k-y) ・・・微分方程式
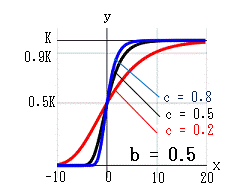
ロジスティック曲線は、上の式を積分したもので、-∞~x の累積関数であり、・・・ロジスティック曲線の式 をグラフにしたものです。 (A = c/K, b = K/y0-1 y0はx=0のy)
ロジスティック曲線の式を検討します。 x→∞ のとき:e-cx→0、分母→1、y→K x→-∞のとき:e-cx→∞、y→0 x=0 のとき:e-cx=1、分母=1+b、y=K/(1+b) になります。 b は、x=0 における高さを決定します。bが同じならば、x=0 における高さは同じです。 cは、曲線の傾きを与えます。 c→0なら、y= K/(1+b) の水平線になります。 c→∞なら、x < 0 で0、x = 0 で 0.5K、x > 0 で1の階段状になります。 微分方程式 dy/dx = Ay(K-y) から、dy/dtが最大になる(増加率が最大になる)のは、 y = K/2 のときです ロジスティック曲線の式から、そのときのxを求めると、 x = log(b)/c (b = 0 なら x = 0) となります。
収束率αとxの関係
y = K になるのは x = ∞ のときですが、実務的には y = 0.99K ならば K に達したといえるでしょう。 ここでは、 y = αk のαを収束率ということにします。= αK これから次の式が得られます。 α = 1/(1+be-cx) x = log(α/(1-α)) / c*log(b) b > 1 -log(α/(1-α)) / c*log(b) b < 1 NuN(±∞) b = 1
x →α b = 0.5 b = 0.9 b = 2.0
c=0.2 c=0.5 c=0.8 c=0.2 c=0.5 c=0.8 c=0.2 c=0.5 c=0.8
x = -5 0.424 0.141 0.035 0.290 0.084 0.020 0.155 0.039 0.009
x = 0 0.667 0.667 0.667 0.526 0.526 0.526 0.333 0.333 0.333
x = 5 0.845 0.961 0.991 0.751 0.931 0.984 0.576 0.859 0.965
x = 10 0.937 0.997 1.000 0.891 0.994 1.000 0.787 0.987 0.999
x = 15 0.976 1.000 1.000 0.957 1.000 1.000 0.909 0.999 1.000
α→x b = 0.5 b = 0.9 b = 2.0
c=0.2 c=0.5 c=0.8 c=0.2 c=0.5 c=0.8 c=0.2 c=0.5 c=0.8
α = 0.5 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
α = 0.9 15.8 6.3 4.0 104.3 41.7 26.1 15.8 6.3 4.0
α = 0.95 21.2 8.5 5.3 139.7 55.9 34.9 21.2 8.5 5.3
α = 0.99 33.1 13.3 8.3 218.1 87.2 54.5 33.1 13.3 8.3
ゴンペルツ曲線(Gompertz curve)
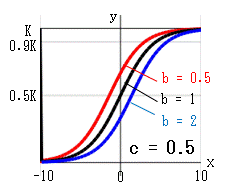
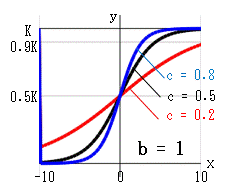
ゴンペルツ曲線は、成長の変化 dy/dx を ・現在の個数に比例して増大する ・時間が経過するのに伴い指数的に減少する の積として捉えます。 dy/dx = A*y*e-cx = -(c*log(b))*y*-cx これを -∞ ~ x まで累積した曲線がゴンペルツ曲線です。(A = -c*log(b) )・・・ゴンペルツ曲線の式 ゴンペルツ曲線は、次の特徴があります。 x→∞ のとき:e-cx→0、b0=1、y→K x→-∞のとき:e-cx→∞、y→b∞→0 x=0 のとき:e-cx=1、y=Kb b, c を変化させたときの曲線の変化を示します。 b:x=0 のときの y を y0 とすれば、y0 = Kb になります。 c:曲線の傾きを示します。 c→大 になると傾きが大になります。 x = 0 は曲線の変曲点でもあります。 b→小、c→小 になると、K値に近ずくまでの時間 x が長くなります。

収束率αとxの関係
例えば、上左図の赤線(b = 0.2, c = 0.5)において、
α = 0.9 (K値の90%)になるのは x = 4 のときで
α ≒ 1 (K値に達する)のは x = 10 になります。
あと 10 - 4 = 6 時間後に成長は止まると考えられます。
 = αK
= αK
より、次の式が得られます。
α = b*e-cx
x = log(log(b)/log(α))/c
x→α b = 0.2 b = 0.5 b = 0.8
c=0.2 c=0.5 c=0.8 c=0.2 c=0.5 c=0.8 c=0.2 c=0.5 c=0.8
x=-5 0.013 0. 0. 0.152 0. 0. 0.545 0.066 0.
x= 0 0.2 0.2 0.2 0.5 0.5 0.5 0.8 0.8 0.8
x= 5 0.553 0.876 0.971 0.775 ★0.945 0.987 0.921 0.982 0.996
x=10 0.804 0.989 0.999 0.910 0.995 1. 0.970 0.998 1.
★ b = 0.5、c = 0.5 の場合は x = 5 で収束値の≒95%に達する
α→x b = 0.2 b = 0.5 b = 0.8
c=0.2 c=0.5 c=0.9 c=0.2 c=0.5 c=0.9 c=0.2 c=0.5 c=0.9
α=0.5 5 2 2 0 0 0 -5 -2 -1
α=0.8 10 4 3 6 3 2 0 0 0
α=0.9 14 6 4 10 4 3 4 2 1
α=0.95 18 7 5 ★14 6 4 8 3 2
α=0.99 26 11 7 22 9 6 16 7 4
★ b = 0.5、c = 0.2 のとき、収束値の95%になるには、x = 14 になる。
ゴンペルツ曲線の変曲点 ((-1/c)*log(-1/log(b)), K*exp(-1))
成長曲線へのあてはめ
実務としては、過去の資料から観測値 (xi, yi) を与えて、ロジスティック曲線やゴンペルツ曲線の係数 K, b, c を統計的手法により決定して計算値を求め、将来の予測をするのが目的になります。
ステップ0 観測データの x と、曲線あてはめでの x の関係
データ測定の観点では、t≧0であり、t0(t=0)のときy=0となりますが、 ロジスティック曲線やゴンペルツ曲線の式では、-∞~∞を対象にしています。 すなわち、生物ははるか昔に発生したというかたちになっています。 それで、x=t+t0とし、t0=-∞ のような加工が必要になります。
係数 k, b, c の決定に関する理論
ステップ1 線形化
ロジスティック曲線 y = K/(1+be-cx について
Y = log(K/(y-1)
X = x
B = log(b)
A = -c
とすると、
Y = AX + B
の線形一次式になります。
ゴンペルツ曲線 y = Kbe-cx では
X = e-cx
Y = log(y)
A = log(K)
B = log(b)
とすると、
Y = AX + B
の線形一次式になります。
ステップ2 A、Bの決定
Y = AX + B での誤差を最小にするには、最小二乗法により A = (nΣXY - ΣXΣY) / (nΣX2 - (ΣX)2) ) B = (ΣY - AΣx) / n で求められます。
ステップ3 各係数の決定
ステップ1の変形を元に戻します。
ロジスティック曲線では、 b = eB, c = -A
ゴンペルツ曲線では、K = eA, b = eB
が得られますし、さらに工夫をして他の係数も算出できます。
実際に求めるには繰返し計算が必要になる
このような手順を示されると、簡単に計算できそうですが、実際には大変な作業になります。 ゴンペルツ曲線を例にします。 ステップ1で x → X を行うのに、この段階では c が未知なので数値化できない ステップ2で X を含む計算ができない。A、Bは未知要素を含んでいる そのため、ステップ3の計算もできない。 これを行うには、 例えば c をある値に設定し、計算を進める それによる計算値と測定値の誤差を調べる cを変更し再計算する というような繰返しを何重にも行うことになります。 この繰り返しを解決する方法もあるのですが、あまりにも高度で複雑です。 Excel の分析ツールや R や Pythonなsどの統計軽量言語の利用を勧めます。
(参考)簡易版計算プログラム
上述の理由により、正攻法での係数決定を諦め、次のような方法を考えました。
x = 0 のときの y を y0, dy/dx を d0 とします。
ここでは (xa,ya)<(xb,yb)<(xc,yc) の3点を通る2次式の x=0 の値を求めます。
y0 = {xc*xb*(xc-xb)*ya + xa*xc*(xa-xc)*yb + xb*xa*(xb-xa)*yc} / {(xa-xb)(xb-xc)(xc-xa)}
d0 = {(xb+xc)(xb-xc)ya + (xc+xa)(xc-xa)yb + (xa+xb)(xa-xb)yc} / {(xa-xb)(xb-xc)(xc-xa)}
曲線の微分による d0 の定式化
ロジスティック曲線の微分方程式 dy/dx = (c/K)*y*(K-y) → d0 = (c/K)*y0*(K-y0)
ゴンペルツ曲線の微分方程式 dy/dx = -c*log(b)*y*e-cx → d0 = -c*log(b)*y0
Kを指定することにすれば、
ロジスティック曲線では、y0 = K/(1+b), d0 = (c/k) y0(K-y0) → b = (k-y0)/y0, c = Kd0/(y0(K-y0))
ゴンペルツ曲線では、 y0 = Kb, d0 = -c log(b)*y0 → b = K/y0, c = -d0/(y0log(b))
により、b, c が定まります。
Kの仮定と最適化
まず K = Kmin = yc とし、dk=Kmin/10 刻みで Kmax=3Kmin まで増加させます。
各 K について ya, yb, yc の計算値 yha, yhb, yhc を計算します。
入力値 y と計算値 yh の偏差平方和 V を計算し、vが最小になる K を決定、改めて b, c を求めます。
このような「雑」な方法ですので、信頼性は怪しいものです。
(ロジスティック曲線とゴンペルツ曲線の式は異なるのですが yh の値は一致します)
少しでも改善するために、3点の設定で、次の前処理が望まれます。
・3点は、xa < 0, xc > 0 にすること
(x = 0 が与えられるなら、もっと単純になりますが、現実にはムリでしょう)
・ya = 0 にすること
ロジスティック回帰分析(Logistic Regression Analysis)
ロジスティック回帰分析の特徴
ロジスティック回帰分析は、質的変数である被説明変数と、量的変数あるいは質的変数である説明変数の関係を 非線形であるロジスティック曲線に当てはめて分析する手法です。 通常の回帰分析は、被説明変数 y は連続量ですが、ロジスティック回帰分析では0/1の2値のケースを扱います。 (2値のときは2値ロジスティック回帰分析といいます。3値、4値を対象にすることもありますが稀です。) ロジスティック回帰分析では非線形の関係ですが、ロジット変形により線形化します。 その線形関係により回帰式を求めます。 回帰式の係数を求めるには、最小二乗法ではなく最尤法を用います。 回帰式で計算した計算値 yh は yh < 0 や yh > 1 になることがあります。 それを防ぐためにロジット変換をして、標本が1になる確率 p を求めます。
ロジスティック回帰分析の前提概念
オッズ(odds)
オッズとは、ある事象 x が起こる可能性を示すもので、発生確率を p (0≦p≦1)とすると、 オッズ = 発生しない確率/発生する確率 = p/(1-p) で定義されます。、 0≦オッズ<1 発生する確率 < 発生しない確率 オッズ=1 発生する確率 = 発生しない確率 1<オッズ<∞ 発生する確率 > 発生しない確率
ロジット(Log Odds = Logit)
ロジットとは、オッズの対数をとったものです。 ロジット = log(p/(1-p)) で定義されます。 -∞<ロジット<0 0 < p < 0.5 ロジット=0 p = 0.5 0≦ロジット<∞ 0.5< p < 1 ロジスティック関数とロジットの関係 ロジスティック関数は、y = K/(1+b*e-cx) で定義されます。 ここで、k = 1, b = 1, c = 1 とすると標準シグモイド関数 y = 1/(1+e-x) その逆関数は、ロジット関数 x = log(y/1-y) になります。 すなわち、標準シグモイド関数はロジットの逆関数で、 ロジスティック関数は、それにパラメタを加えて一般化したものです。
オッズ比(Odss Ratio)
事象 x0 の起こる確率を p0, x1 の起こる確率を p1 としたときのオッズの比率で オッズ比 = (p0/(1-p0)) / (p1/(1-p1)) で定義されます。 0≦オッズ比<1 x0の発生確率 < x1の発生確率 事象が x0 で起こりやすい オッズ比=1 x0の発生確率 = x1の発生確率 事象の起こりやすさは x0, x1 で同じ 1<オッズ比<∞ x0の発生確率 > x1の発生確率 事象が x1 で起こりやすい 喫煙と肺がんの関係で、次のデータがあるとします。 喫煙者 非喫煙者 合計 肺がん確率 肺がんの人 40 10 50 p0 = 40/50 = 0.8 健康な人 20 80 100 p1 = 20/100 = 0.2 オッズ比 = (p0/(1-p0)) / (p1/(1-p1)) = (0.8/0.2)/(0.2/0.8) = 16 健康な人と比べて、肺がんの人では喫煙者が肺がんである可能性が非喫煙者の16倍になる
ケース1
ケース2
ロジスティック回帰分析の方法
ロジスティック回帰分析とは、
被説明変数を y, 説明変数を x(複数)とし、yの確率を p としたとき
p = 1/(1+e-L) L = α + β0x0 + β1x1 + β2x2 + …
で近似するαとβiを決定します。
(「ジグモイド回帰分析」というべきかもしれません)
上式を変形すると
log(p/(1-p)) = L = α + β0x0 + β1x1 + β2x2 + …
となります。ここにロジットが現れます。
これを標本データの形式に置き換えると、
y[j] = α + βiΣx[i][j]
となり、線形化できます。
これから、何らかの手段により、α + βi を決定し(注)回帰式を求まることができます。
α、βi が決定すれば、y[j] の計算値 yh[j] が計算でき、
さらに yh[j] = log(p[j]/(1-p[j])) から、p[j] を求めることができます。
(注)通常の回帰分析では、y が連続量であり、最小二乗法を用いて回帰式を求めますが、
ロジスティック回帰分析では2値変数なので、最尤法という方法を用います。
参照:「Python によるロジスティック回帰・予測」
(しかし、最尤法の処理方法は複雑ですので、次の例題では最小二乗法を用いています)
例題
結果の吟味
p の意味
y = 1 になる確率です。標本0では43.8%、標本9では77.4%になります。
回帰式の係数β
β>0ならば yh が大に、p が大になります。
pを大にするためには、x[0], x[1] を大に、x[2] を小にする(0にする)のが適切です。
オッズ比
例えば x[0] で4以上と3以下の2群に分けてみます。
合計 y=1 y=0 p オッズ
4以上 5(2,5,7,8,9) 4(5,7,8,9) 1(2) 4/5=0.8 0.8/0.2 = 4
3以下 5(0,1,3,4,6) 1(6) 4(0,1,3,4) 1/5=0.2 0.2/0.8 = 0.25
オッズ比 = 4/0.25 = 16
→ x[0] ≧ 4 であることは、y = 1 になることに大きく影響する