スタートページ>
Javascript>
CANVAS>
物理等
流体力学 球形タンクからの排水時間と水位
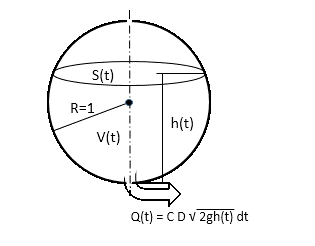
水の入っている球形タンクの底部から水を流出させます。満水の状態から空になる液面高さの変化を求めたいのです。
R = 1 [m} 球形タンクの半径
D = 0.01 [m] 排水孔の断面積
C = 0.8 [-] 排水効率
高さ1から0になるまでが15分になるように D を指定してください。
(解説)
解説
- エネルギ保存則から、流出速度は √(2gh) [m/s] になります。
流水孔の面積を D [m2]、流出効率を C [-] とすると、微小時間 dt [s] に流出する量は
Q = C D √(2gh) dt [m3]
になります。
- 一方、高さhの水面の半径 r は、r2 = R2 - (h-R)2 = h(2R-h) ですから、水面の面積は、
S = (π/4)r2 = (π/4) h(2R-h)
となり、dt の間に dh [m] だけ水位が下がるとすれば、その水量は
V = -S dh = -(π/4) h(2R-h) dh [m3]
になります。
- Q = V ですから、C D √(2gh) dt = -(π/4) h(2R-h) dh
∴ dh = -C D √(2gh)/ (π/4) h(2R-h)*dt = -(4CD√2g /π)*(1/(2R-h)√h)*dt
この定数項を A = (4CD√2g /π)とすれば、
dh = -A/(2R-h)√h * dt 式1
となります。
- 初期値を、t=0のときタンクが満水とすると、h=2R となり dh=∞ となってしまいます(タンクの頂上では断面積が0なので、水面低下速度が∞になることからも推察できます)。それで次のように考えます。
初期値の水位をタンクの中央である(h0 = r)とすれば、式1は dh =-R-3/2 dt となります。t>0 の水位はこれから計算できます。
上半分(t<0)については、Qと同じ水量をタンク上部から注水して水位の上昇を計算するならば、式1は dh =-R-3/2 dt となります。
- ここで
g = 9.81 [m/s2] 重力
R = 1 [m} 球形タンクの半径
D = 0.01 [m] 排水孔の断面積
C = 0.8 [-] 排水効率
を代入すると、
A = 0.8*0.01*√2*9.81/3.14 = 0.03534
となります。
