力学　ケプラーの法則

主要変数

与件
　　e　離心率　
　　T　公転周期　　
求値(一定値)
　　a　長半径　
　　b　短半径　b = a*Math.sqrt(1-e*e)
　　ae　焦点位置　ae = a*e
　　pe　近日点の太陽からの距離　pe = a-ea
　　ap　遠日日点太陽からの距離　ap = a+ea

求値（t=0～T における）
　　ｕ　ｔにおける離心近点離角
　　Ｘ　原点０からの衛星のＸ値
　　Ｙ　原点０からの衛星のＹ値
　　ｒ　焦点からの衛星の距離
　　θ　焦点から見た角度
　　ｖ　衛星の角速度

第３法則（調和の法則）

与件の公転周期 T から 長半径 a を求める。
　　Ｇ：万有引力定数 6.67408×10-11 [m3/㎏*s2]
　　Ｍ：太陽の質量 1.98892×1030 [kg]
注
　実際の値を用いるとスケールが大になるので、ここではＧＭ＝4π2とする。
　地球の公転周期 = 365[日] だが、ここでは与件として、T = 1 程度とする。

公式
　　a3 / Ｔ2 = ＧＭ / 4π2　(=1)
　　（T=1 なら a=1)

第１法則（楕円軌道の法則）

離心率が与件で、長半径 a が得られたので、求値(一定値)が計算できる、
　　a　長半径　
　　b　短半径　b = a*Math.sqrt(1-e*e)
　　ae　焦点位置　ae = a*e
　　pe　近日点の太陽からの距離　pe = a-ea
　　ap　遠日日点太陽からの距離　ap = a+ea

第２法則（面積速度一定の法則）

T における離心近点離角 u の計算

第１法則から
原点Ｏを基準とした楕円の式　(X/a)2 + (Y/b)2 = 1　を
　　Ｘ=a*cos(u)
　　Ｙ=b*sin(u)
と変形する。
この u は、原点から見た衛星の角度であり、離心近点離角という。参考図
第２法則から　tにおける u が得られる。
　　面積速度　S=(1/2)rv*sin(θ) = 一定
　　角運動量保存則　dS/dt = (1/2)a*a*sqrt(1-e*e)(1-e*cos(u)) * du/dt  
による複雑な計算の結果、
　　u-e*sin(u) = (2π/T)*t
の関係が得られる。計算が面倒だが、t における u の値が得られる。

u から、各種の計算をする

ｒ：t=t における惑星と焦点の距離
　　r =  a(1-e*cos(u));
X,Y 原点Ｏを基準とした座標
　　Ｘ=a*cos(u)
　　Ｙ=b*sin(u)
θ：焦点から見た衛星の角度
　　tan(θ）= Y/(X-ea)
ｖ：t=t における惑星の角速度
　　v = (θ(t+dt) - θ(t)) / dt

u-e*sin(u) = (2π/T)*t の求解

    f(x) = x - e*sin(x) - C*t = 0　　C = (2π/T)
をニュートン法で解く。
条件
　　0 < x < 2π
　　微分　g(x) = 1 - e*cos(x)
　　0 < e < 1　なので　0 < 1-e < g(x) < 1+e の単調増加関数
　　t=0 のとき f(x) = 0
　　初期値は t=t-1 の解を用いればよい。

実際の諸元

万有引力定数　Ｇ　6.67408×10-11 [m3/㎏*s2]
太陽の質量　　Ｍ　1.98892×1030 [kg]
                                    地球      火星
離心率　　  e　                     0.0167    0.0934
公転周期    T [日]                  365.9     687.0
長半径　　  a　106[km]   149.6     227.9
近日点距離  pe 106[km]   147.1     206.7
遠日点距離  ap 106[km]   152.1     249.2

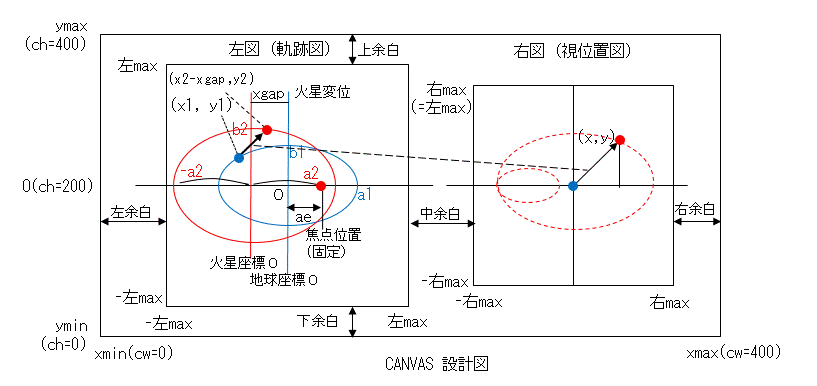
前の「ケプラーの法則」と重要な違いは、前は太陽（焦点）の位置を ae = a*e （長半径*離心率）としていましたが、地球も火星も同一の焦点の周りを巡るのですから、ae を固定する必要があります。そのため、地球を基準とした座標系で、火星軌道の原点を　xgap = a2-ae/e2　だけ変位して考えることになります。
それ以外は、以前と同様にして地球（青色）と火星（赤色）の軌道を計算して左図を作図できます。
地球の位置を(x1,y1), 火星の位置を(x2,y2) として、x = x2-x1, y = y2 - y1 を求め (x.y) をプロットしたのが右図です。周期的に複雑な動きをします（惑星！）

プログラムでは、左図と右図を同一CANVASにするため、CANVASの設計が複雑になります。図はその設計図です。