スタートページ＞ JavaScript＞ ライブラリ目次

確率関連 JavaScript関数ライブラリ stat.js の利用解説書

ご利用にあたって

基本統計量（１変数）
　　rtn = statBasic(x);　コード表示

配列 x を入力して次の基本統計量を得る。
参照：「平均、分散、標準偏差」

ケース１

入力
　　var x = [40, 20, 50, 10, 30];
　　var rtn = statBasic(x);
出力
    rtn["標本数"] =　　 5　　　　n
    rtn["最小値"] =　　 10
    rtn["最小値位置"] =　3       最小値が x[i] の i。複数あるときはは最早発生
    rtn["最大値"] =　　 50
    rtn["最大値位置"] =　2       最大値が x[i] の i。複数あるときはは最早発生
    rtn["範囲"] =　　　 40　　　 最大値 - 最小値
    rtn["合計"] =　　　 150　　　Σx
    rtn["平均"] =　　　 30　　　 μ = Σx／n
    rtn["平方和"] =　　 5500　　 Σx2
    rtn["偏差平方和"] = 1000　　 Σ(x-μ)2 = Σx2 - (Σx)2/n
    rtn["不偏分散"] =　 250　　　σ2 = 偏差平方和/(n-1)
    rtn["標準偏差"] = 　15.81　　σ = √不偏分散
    rtn["変動係数"] =　 0.527　　標準偏差/μn

ケース２

基本統計量（パーセント点）
　　rtn = statBasicPer(x ,p);　コード表示

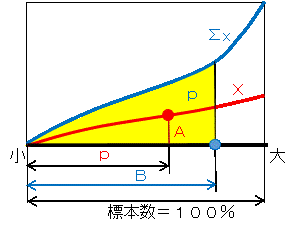
パーセント点とは、標本 x を昇順に並べたときに、指定した p よりも小さな標本の割合が p である x[i] の値 Ａ のこと。
p = 0.25, 0.50, 0.75 の x[i] を、第１四分位点、中央値（メジアン）、第３四分位点という。
さらに、x[i] の累計の割合が p となる件数の割合 Ｂ も算出している。
ここでは、p を小数点で表示、複数個を与えることができる。

ケース１

入力
    var x = [ 34, 44, 20, 32, 50, 31, 20, 45, 20, 10,
              43, 23, 33, 52, 33, 29, 46, 22, 12, 30,
              20, 30, 54, 35, 20, 48, 21, 12, 36, 26,
              30, 56, 35, 26, 40, 20, 14, 30, 24, 41,
              58, 30, 20, 42, 20, 14, 30, 23, 42, 30,
              30, 24, 43, 27, 15, 30, 21, 44, 37, 60,
              21, 46, 20, 14, 30, 20, 47, 38, 61, 30,
              40, 20, 17, 30, 20, 49, 39, 62, 38, 20,
              22, 16, 30, 28, 40, 30, 63, 35, 25, 40,
              15, 35, 20, 41, 31, 64, 33, 23, 43, 20 ];
    var p = [ 0.25, 0.5, 0.75, 0.9 ];
    var rtn = statBasicPer(x, p);
出力
    与えたｐ          説明のＡ        説明のＢ
    rtn[0][0]=0.25　　rtn[0][1]=21　　rtn[0][2]=0.4
    rtn[1][0]=0.5　　 rtn[1][1]=30　　rtn[1][2]=0.65
    rtn[2][0]=0.75　　rtn[2][1]=41　　rtn[2][2]=0.85
    rtn[3][0]=0.9　　 rtn[3][1]=50　　rtn[3][2]=0.94

ケース２

基本統計量（２変数）
　　rtn = statBasic2(x,y);　コード表示

配列 x, y を入力して次の基本統計量を得る。

ケース１

入力
    var x = [26, 25, 23, 27, 28, 25, 22, 26, 25, 23];
    var y = [54, 62, 51, 58, 63, 65, 59, 63, 65, 60];
    var ary = statBasic(x, y);
出力（Ｘ、Ｙは大文字全角で）
    rtn["標本数"] = 　　　10 　　　n
    rtn["合計Ｘ"] = 　 　 250　　　Σ(x)
    rtn["合計Ｙ"] = 　 　 600　　　Σ(y)
    rtn["平均Ｘ"] = 　　　25 　　　μx = Σ(x)/n
    rtn["平均Ｙ"] = 　　　60 　　　μy = Σ(y)/n
    rtn["平方和Ｘ"] = 　　6282 　　Σ(x2)
    rtn["平方和Ｙ"] = 　　36194　　Σ(y2)
    rtn["積和"] = 　　　　15023　　Σ(x・y)
    rtn["偏差平方和Ｘ"] = 32 　　　Sxx = Σ(x-μx)2
    rtn["偏差平方和Ｙ"] = 194　　　Syy = Σ(y-μy)2
    rtn["偏差積和"] = 　　23 　　　Sxy = Σ(x-μx)(y-μy)
    rtn["共分散"] = 　　　2.556　　Sxy/(n-1)
    rtn["回帰係数Ｘ"] = 　0.718　　Bx = Sxy/Sxx　　y = a + bx のｂ
    rtn["回帰係数Ｙ"] = 　0.119　　By = Sxy/Syy　　x = a + by のｂ
    rtn["寄与率"] = 　　　0.085　　r2 = Bx・By
    rtn["相関係数"] = 　　0.291　　r = √(r2)
    rtn["勾配"] =         0.719    回帰係数Ｘ                 y = a + bx の b
    rtn["Ｙ定数項"] =     42.03    (Σ(y) - Σ(x)*勾配) / n   y = a + bx の a
    rtn["Ｘ定数項"] =     42.03    (Σ(x) - Σ(y)*回帰係数Ｙ) / n   x = a + by の a
　回帰式：y = Ｙ定数項 + 回帰係数Ｘ * x = 42.03 + 0.719 x
　　　　　x = Ｘ定数項 + 回帰係数Ｙ * y = 17.89 + 0.119 y

ケース２

頻度表（１変数）
　　rtn = statHist1(x, bx);　コード表示

一次元配列 x[i]　(i=0～m) と、境界値 bx[j]　(j=0～n) を与えて, bx[j] ≦ x ＜ bx[i+1] となる x の頻度 hx[i] （ x ＜ bx[0] なら hx[0]. bx[n] ≦ x なら hx[n+1] ）を集計、一次元配列 h[j]　(j=0～n+1) を戻します。

入力
    var x = [ 0.0, 0.2, 0.4,                                    // hx[0] =  3
              0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4, // hx[1] = 10
              2.6, 2.8, 3.0, 3.2, 3.4, 3.6, 3.8, 4.0, 4.2, 4.4, // hx[2] = 10
              4.6, 4.8, 5.0, 5.2, 5.4, 5.6, 5.8 ];              // hx[3] =  7
    var bx = [ 0.5, 2.5, 4.5 ];                                  // 昇順に並べる
出力
    var hx = statstatHist1(x, bx);
    // hx[0] = 3, hx[1] = 10, hx[2] = 10, h[3] = 7

頻度表（２変数）
　　rtn = statHist2(x, y, bx, by);　コード表示

上の statHist1 を２次元に拡張したものです。

入力
    var x = [ 0.0, 0.2, 0.4,
              0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.4,
              2.6, 2.8, 3.0, 3.2, 3.4, 3.6, 3.8, 4.0, 4.2, 4.4,
              4.6, 4.8, 5.0, 5.2, 5.4, 5.6, 5.8 ];
    var y = [   1,   2,   4,
                1,   1,   1,   2,   2,   2,   4,   4,   4,   4,
                1,   1,   1,   1,   1,   2,   2,   4,   4,   4,
                1,   1,   2,   2,   4,   4,   4 ];
    var bx = [ 0.5, 2.5, 4.5 ];
    var by = [ 1.5, 3.5 ];
出力
    var hxy = statHist2(x, y, bx, by);
　hxy[jx,jy]
    jx jy=0　1　2　計
     0　　1  1  1　 3
     1　　3  3  4　10
     2　　5  2  3　10
     3　　2  2  3　 7
    計　 11　8 11　30

共分散行列・相関行列
　　statCovcorTrace(表示場所, x)　コード表示
　　rtn = statCovcor(x)　コード表示

    rtn["共分散行列"]
    rtn["相関行列"]

ケース１

入力
　　　　　　　　標本 x[*][k]
    var x = [[12, 20, 24, 26, 33],   ┐
             [ 3,  6,  7, 10, 14],　 ├　系列 x[i][*]
             [22, 16, 14, 19,  8]];  ┘
    var rtn = statCovcor(x);
出力
  rtn["共分散行列"]
     [[ 60,    31.5, -34.75],
        31.5,  17.5, -17.5],
       -34.7, -17.5,  28.2]]
  rtn["相関行列"]
    [[  1,     0.972, -0.844],
     [ 0.972,  1,     -0.787],
     [-0.844, -0.787,  1    ]]

ケース２

順列の数　nＰr の値　　 nＰr = n(n-1)(n-2)…(n-r+1)
　　nPr = statNPR(n, r) 　コード表示

組合せの数　nCr の値　　 nCr = n(n-1)(n-2)…(n-r+1) / r(r-1)(r-2)…1
　　nCr = statNCR(n, r) 　コード表示

nCｒ の全組合せの列挙
　　statClistTrace(表示場所, n)　コード表示
　　list = statClist(n)　コード表示

要素 0. 1. 2. …, n-1 のｎ個から、ｒ個を取り出す組み合われ nCr の全リストを列挙する
[r][i][j] r:選択数、i：リスト番号、j：選択要素
例  statClist(4)
list[0]　リスト数=0
list[1]　リスト数=4
　    list[1][0]=0      list[1][1]=1　    list[1][2]=2　    list[1][3]=3
list[2]　リスト数=6
　    list[2][0]=0,1　  list[2][1]=0,2　  list[2][2]=1,2　  list[2][3]=0,3　  list[2][4]=1,3　list[2][5]=2,3
list[3]　リスト数=4
　    list[3][0]=0,1,2　list[3][1]=0,1,3　list[3][2]=0,2,3　list[3][3]=1,2,3
list[4]　リスト数=1
　    list[4][0]=0,1,2,3

ケース１

    var list = statClist(5):

ケース２

ベイズの定理

ベイズの定理　周辺確率
　　statBayes1Trace(表示場所, 客観確率[, 事象発生])　コード表示
　　事後確率 = statBayes1(客観確率[, 事象発生])　コード表示

m 個の独立した原因があり、それぞれの原因により発生する n 個の結果の発生確率が与えられています。
このとき、結果 j が実現したとき、その原因が i である確率（事後確率）を求めよという問題です。
その発展として、結果 j1 と結果 j2 が同時に起こったとき、原因 i である確率も求めます。
このときは「発生」を指定します。
参照：ベイズの定理

問題
　野球（Ａ）、サッカー（Ｂ）、ラグビー（Ｃ）のスポーツ（原因）に関する多数の文章を対象にして、
　ボール（Ｘ）、ファール（Ｙ）、ゴール（Ｚ）のキーワード（結果）の有無を発生確率にして表にしました。
　（野球に関する１０文書のうち、７文書に単語「ボール」があれば 0.7 とします）
　ある文章に、「ボール」がありました。この文章が野球に関する文章である確率は？
　「ボール」と「ファール」がある文章なら、どのスポーツの文章でしょうか？
問題
　３つの病気Ａ，Ｂ，Ｃがあり、各病気には症状Ｘ，Ｙ，Ｚがあり、例えばＡのときＸが起こる確率は 0.7 
  というような統計資料がある。診断したら症状ＸとＹがあった。Ａである確率は？ 

ケース１

入力
                        X     Y    Z
    var 客観確率 = [ [ 0.7,  0.6, 0.1],     // A
                     [ 0.3,  0.4, 0.6],     // B
                     [ 0.4,  0.5, 0.3] ];   // C
    var 事象発生 = [ [  1,    1,   0 ],     // 出現単語を１とする　「ボール」と「ファール」が出現した場合
                     [  1,    0,   1 ] ];
    var p = statBayes1(客観確率, 事象発生); // 事後確率
出力
　　　　　　　　X              Y              Z             XY             XZ
　0(A)    p[0][0]=0.5    p[0][1]=0.4    p[0][2]=0.1   p[0][3]=0.568  p[0][4]=0.189
　1(B)    p[1][0]=0.214  p[1][1]=0.267  p[1][2]=0.6   p[1][3]=0.162  p[1][4]=0.486
　2(C)    p[2][0]=0.286  p[2][1]=0.333  p[2][2]=0.3   p[2][3]=0.27   p[2][4]=0.324
    ある文書に単語「ホール」があれば、野球に関する文書である確率は 0.5、「ボール」と「ファール」があれば 0.568

ケース２

ベイズの定理　原因推測
　　statBayes2Trace(表示場所, 事前確率, 客観確率[, 事象発生])　コード表示
　　事後確率 = statBayes2(事前確率, 客観確率[, 事象発生])　コード表示

問題
　statBayes1 において、Ａ，Ｂ，Ｃである確率（事前確率）が、0.2, 0.3, 0.5 であると想定されているとします。
　それを、キーワードの出現確率を用いて事後確率にしたいのです。
　statBayes1 との違いは、事前に来る割合がわかっているということですが、
　出現確率に事後確率を乗ずるだけで、考え方は statBayes1 と同じです。
　参照：ベイズの定理

ケース１

入力
                        A    B    C
    var 事前確率 =   [ 0.2, 0.3, 0.5];    // 合計=1

                        X     Y    Z
    var 客観確率 = [ [ 0.7,  0.6, 0.1],     // A
                     [ 0.3,  0.4, 0.6],     // B
                     [ 0.4,  0.5, 0.3] ];   // C
    var 事象発生 = [ [  1,    1,   0 ],     // X, Y が同時に発生する場合も計算する
                     [  1,    0,   1 ] ];   // X, Z が同時に発生する場合も計算する
     // 複数の条件を与えないなら「事象発生」を与えない

    var 事後確率 = statBayes2(事前確率, 客観確率);
出力
            X              Y              Z             XY             XZ
　A   [0][0]=0.326   [0][1]=0.245   [0][2]=0.057   [0][3]=0.216   [0][4]=0.057
　B   [1][0]=0.209   [1][1]=0.245   [1][2]=0.514   [1][3]=0.139   [1][4]=0.331
　C   [2][0]=0.465   [2][1]=0.51    [2][2]=0.429   [2][3]=0.644   [2][4]=0.612

　ある文書が野球関連文書である確率は 0.2 と思っている（事前確率）
　文書にキーワード「ボール(x)」と「ファール(Y)」が入っていた。
　それにより、野球関連文書である確率は 0.216 に上昇した（事後確率）

ケース２

ベイズの定理　ベイズ推測
　　statBayes3Trace(表示場所, 事前確率, 客観確率)　コード表示
　　事後確率 = statBayes3(事前確率, 客観確率)　コード表示

問題
　　伝染病対策として感染の検査を行いますが、その結果が１００％正確だとはいえません。
　　感染している人が、検査では陰性になったり（偽陰性率）、感染していない人が陽性となったり（偽陽性率）します。
　　それらが、どの程度であるかを知りたいのです。
　　（同じようなことに、天気予報が晴といったのに雨になったり、雨と予報したのに晴れることがあります。）
ベイズ推測
　　ある事象 i が発生する主観確率（事前確率）を P(Hi),　検査や予報で得た確率（客観確率）を P(Di) 
    主観で i だとしたことが検査でも i となる確率を P(Di|Hi)
    検査の結果が i だと出たとき、主観確率も考慮した事後確率を P(Hi|Di) としたとき、
　　　Ｐ(Hi|D) ＝ Ｐ(Hi)*Ｐ(Di|Hi) / ΣＰ(Hi)*Ｐ(Di|Hi)
    で計算できます。
    これを用いて事後確率を求めることをベイズ推測といいます。
参照：ベイズの定理

ケース１

ある病気について、次のような確率があったとします。
　・全集団では感染者と非感染者の割合（事前確率、主観確率）は3%と97%といわれている（実際には不明）。
　　　　P(H0) = 0.03
　　　　P(H1) = 1-P(H0) = 0.97
　・これまでの統計から、正しく感染者と判明している人の検査では、98%が陽性、2%が陰性と診断される（客観確率）。
　　　　P(D0|H0) = 0.98
　　　　P(D1|H0) = 1-0.98 = 0.02
　・同様に、正しく非感染者と判明している人の検査では、95%が陰性、5%が陽性と診断される（客観確率）。
　　　　P(D0|H1) = 0.05
　　　　P(D1|H1) = 1-0.05 = 0.95
これから、次の確率（事後確率）を計算します。
　　　　　　　　　　　　主観　　検査　　事後確率
　　感度（真陽性率）　　感染　　陽性　　P(H0|D0)
　　特異度（真陰性率）　非感染　陰性　　P(H1|D1)
　　偽陽性率　　　　　　非感染　陽性　　P(H1|D0)
　　偽陰性率　　　　　　感染　　陰性　　P(H0|D1)

入力
　  var PH = [ 0.03,    // P(H0)
               0.97 ];  // P(H1)
          合計=1
                  D0    D1
    var PDH = [ [ 0.98, 0.02 ],   // 合計=1　P(D0|H0) = PDH[0][0], 　P(D1|H0) = PDH[0][1],
                [ 0.05, 0.95 ] ]; // 合計=1　P(D0|H1) = PDH[1][0], 　P(D1|H1) = PDH[1][1],
    var PHD = statBayes3(PH, PHD);
出力
　　P(H0|D0) = PHD[0][0] = 0.377　　感染者と思われる人が陽性と判定される確率(真陽性率)
　　P(H0|D1) = PHD[0][1] = 0.001　　感染者と思われる人が陰性と判定される確率(偽陰性率)
　　P(H1|D0) = PHD[1][0] = 0.623　　非感染者と思われる人が陽性と判定される確率(偽陽性率)
　　P(H1|D1) = PHD[1][1] = 0.999　　非感染者と思われる人が陰性と判定される確率(真陰性率)
（注）
  偽陽性率が大きいのは、事前確率での感染率 P(H01) が小さいからです。
  「ほとんどが非感染者なので陽性になることはめったにない」のに
　「めったにないことが発生した」ことが大きく影響したのです。

ケース２