スタートページ> JavaScript> 他言語> Python 目次> ←主成分分析 →クラスター分析
下記の青線の部分をGoogle Colaboratryの「コード」部分にコピーアンドペースト(ペーストは Cntl+V)して実行すれば、右図の画像が表示されます。
特性 c0,c1,c2,… をもつ多数のデータ群 A,B,C,… を、あらかじめグループ群(正群、負群)に区分しておき、それに統計的処理をするとにより、
Z = b0*c0 + b1*c1 + b2*c2 +…
の b0.b1.b2,… を決定します。
そして、新データが与えられたとき、Zを計算して、Z>0ならば正群、Z<0ならば負群に属しると判別します。
このような統計的方法を判別分析といい、Zを判別関数といいます。判別関数を算出する方法はいくつかありますが、代表的なものにフィッシャーの判別関数があります。
ここでは、各行に判別値(group)として1と-1を与え、c0~c5 の値から判別関数Zを作成します。 numpy.linalg や sklearn などのライブラリが用いれれていますが、その説明は「主成分分析」(pca.txt) を参照してください。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# ================================ 入力データ
df = pd.DataFrame([
['A',-1, 3, 4, 4, 5, 4, 4],
['B',-1, 6, 6, 7, 8, 7, 7],
['C', 1, 6, 5, 7, 5, 5, 6],
['D',-1, 6, 7, 5, 4, 6, 5],
['E', 1, 5, 7, 6, 5, 5, 5],
['F',-1, 4, 5, 5, 5, 6, 6],
['G', 1, 6, 6, 7, 6, 4, 4],
['H',-1, 5, 5, 4, 5, 5, 6],
['I', 1, 6, 6, 6, 7, 7, 6],
['J', 1, 6, 5, 6, 6, 5, 5],
['K',-1, 5, 4, 4, 5, 5, 5],
['L', 1, 5, 5, 6, 5, 4, 5],
['M', 1, 6, 6, 5, 5, 6, 5],
['N', 1, 5, 5, 4, 4, 5, 3],
['O',-1, 5, 6, 4, 5, 6, 6],
['P', 1, 6, 6, 6, 4, 4, 5],
['Q',-1, 4, 4, 3, 6, 5, 6],
['R', 1, 6, 6, 7, 4, 5, 5],
['S',-1, 5, 3, 4, 3, 5, 4],
['T', 1, 4, 6, 6, 3, 5, 4]],
columns = ['name','group','c0','c1','c2','c3','c4','c5'])
# =========== グループ別の行列に変換
# group の正負により、正群x1と負群x2に分割、計算に用いる列だけを取り込み
# ndarray に変換
x = df[['c0','c1','c2','c3','c4','c5']].values
x1 = df[df.group > 0].loc[:,['c0','c1','c2','c3','c4','c5']].to_numpy() # 正群
x2 = df[df.group < 0].loc[:,['c0','c1','c2','c3','c4','c5']].to_numpy() # 負群
# =========== 諸元の算出
n1 = len(x1) # x1 の要素数
n2 = len(x2) #
m1 = np.mean(x1, axis=0) # x1 の平均
m2 = np.mean(x2, axis=0) #
m = (m1*n1+m2*n1)/(n1+n2) # 全体の平均
#
# ========================= 判別関数の計算
#
import numpy.linalg as LA
sw = ((x1-m1).T @ (x1-m1)) + ((x2-m2).T @ (x2-m2))
sinv = np.linalg.inv(sw)
w = -sinv @ (m2 - m1)
print('重み:w = ', w)
print('平均:m = ', m)
print('判別関数:Z = w[0]*(c0-m[0]) + w[1]*(c1-m[1]) + w[2]*(c2-m[2]) + …; >0なら正群 <0なら負群')
# ============= 元配列に判別関数をあてはめる
df['Z'] = np.dot(x-m, w)
df['err'] = ' '
df.loc[(df.group * df.Z < 0), 'err'] = '×'
print(df)
# ============= 判別関数の算出としてはこれまでです
# 以降は図の作成のためです。
#
# 主成分分析
from sklearn.decomposition import FactorAnalysis as FA
corr = df.corr() # 共分散行列
eig, eigv = np.linalg.eig(corr) # eig 固有値
fa = FA(n_components=2, max_iter=500)
fa.fit(x)
df['f1'] = fa.fit_transform(x)[:,0] # 第1因子の値
df['f2'] = fa.fit_transform(x)[:,1] # 第2因子の値
# 散布図作成
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
df.loc[df['group'] > 0, 'color'] = 'b'
df.loc[df['group'] < 0, 'color'] = 'r'
ax.scatter(df.f1, df.f2, color=df.color)
for i, txt in enumerate(df.name):
ax.annotate(txt, (df.f1[i], df.f2[i]), size=14)
ax.grid()
ax.plot([-3,3],[0,0], color='k', linewidth=1)
ax.plot([0,0],[-2,2.5], color='k', linewidth=1)
fig.show()
判別関数の決定
重み:w = [ 0.060 0.045 0.102 0.015 -0.050 -0.118 ]
平均:m = [ 5.677 5.838 5.744 5.511 5.744 5.644 ]
判別関数:Z = w[0]*(c0-m[0]) + w[1]*(c1-m[1]) + w[2]*(c2-m[2]) + …;
>0なら正群 <0なら負群
元データへの当てはめ
name group c0 c1 c2 c3 c4 c5 Z err
0 A -1 3 4 4 5 4 4 -0.146
1 B -1 6 6 7 8 7 7 -0.031
2 C 1 6 5 7 5 5 6 0.097
3 D -1 6 7 5 4 6 5 0.036 ×
4 E 1 5 7 6 5 5 5 0.144
5 F -1 4 5 5 5 6 6 -0.277
6 G 1 6 6 7 6 4 4 0.445
7 H -1 5 5 4 5 5 6 -0.269
8 I 1 6 6 6 7 7 6 -0.030 ×
9 J 1 6 5 6 6 5 5 0.129
10 K -1 5 4 4 5 5 5 -0.195
11 L 1 5 5 6 5 4 5 0.104
12 M 1 6 6 5 5 6 5 0.006
13 N 1 5 5 4 4 5 3 0.071
14 O -1 5 6 4 5 6 6 -0.274
15 P 1 6 6 6 4 4 5 0.194
16 Q -1 4 4 3 6 5 6 -0.461
17 R 1 6 6 7 4 5 5 0.246
18 S -1 5 3 4 3 5 4 -0.152
19 T 1 4 6 6 3 5 4 0.127
・group と Z が異なる符号ならば、元データがこの判別関数に合致しなかったことを示します。
20件中、合致しなかったのはDとIの2件なので、この判別関数は適切だといえます。
・Zの絶対値が大ならば、明らかにその群に属するといえます。
0に近いものは、「どちらかといえばその群になるが、他の群である可能性は否定できない」といえます。
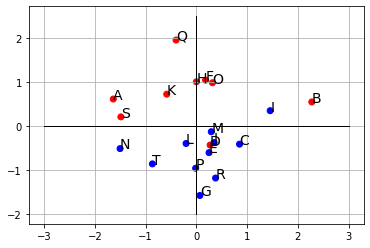
・この関係を可視化するとグラフになります。