シャドウ・プライスとレンジ

　　　　目的関数
　　　　　Ｚ＝３ｘ_１＋２ｘ_２　→　最大
　　　　制約条件
　　　　　　　４ｘ_１＋１ｘ_２≦７２
　　　　　　　２ｘ_１＋２ｘ_２≦４８
　　　　　　　１ｘ_１＋３ｘ_２≦４８
　　　　　　　ｘ_１≧０，ｘ_２≧０

この問題を図式解法およびシンプレックス法により解くと次のようになりました。

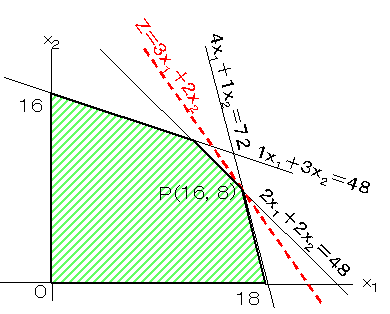
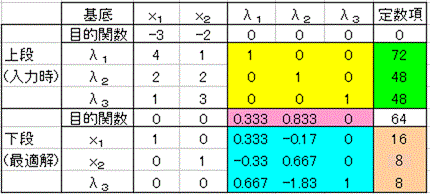
シャドウ・プライス

Reduced cost、潜在価格ともいいます。下段の目的関数の行では，λ_１が０.３３，λ_２が０.８３でプラスになっています。これは，λ_１を１だけ作ると目的関数が０.３３だけ「減少」することを示しています。λ_１を１作るということは，４ｘ_１＋１ｘ_２＋１λ_１＝７２においてλ_１＝１として，４ｘ_１＋１ｘ_２＋＝７１としたことに一致します。

これをグラフで見ると，青色の太線４ｘ_１＋１ｘ_２＋＝７２のときは，最適解はＰ点であり，目的関数は赤の太線でした。それが，４ｘ_１＋１ｘ_２＋＝７１になると青色の点線になるので，最適解はＱに移動して，目的関数は赤の点線になります。この赤の太線が点線に移動したときの目的関数の値の減少が０.３３なのです。

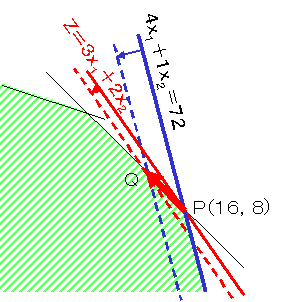
さらに物理的な意味では，λ_１の在庫が１だけ少ないと０.３３だけ利益が減少することであり，逆にいえば，λ_１の価格が０.３３よりも安ければ購入しｘ_１やｘ_２を増産したほうがよいということです。それでこの０.３３をλ_１のシャドウ・プライスといいます。

それに対してλ_３は目的関数の値が０です。これは在庫が減っても増えても利益には関係しないことを示しています。それは最適解がλ_３＝８であり，この制約条件に余裕があることと一致します。ですから，λ３のシャドウ・プライスは０になります。

このシャドウ・プライスの概念は，会計学での限界費用に似た概念であり，制約条件の余裕の有無により価値が変化するという，非常に重要な概念なのです。

定数項の変化とレンジ

制約式の定数項の値が変化しても、基底が変化しない範囲を求めます。

基底にない場合

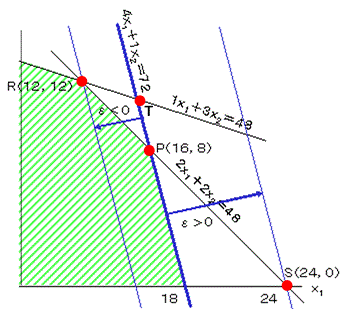
制約式 λ_１：４ｘ_１＋１ｘ_２≦７２を例にします。λ_１は基底に入っていません。すなわち。定数項の値７２を使い切っており余裕はない状態です。

グラフでの説明

まずグラフで説明しましょう。制約式：４ｘ_１＋１ｘ_２≦７２を例にします。青色の太線で最適値はＰ点でした。この７２をεだけ、変化させることを考えます。
　この定数項７２を減少する（ε＜０）と、最適値は直線ＰＲにそって移動します。Ｒ点に達して（定数項＝６０．ε＝－１２）それを超えると，いままで余裕のあった１ｘ_１＋３ｘ_２≦４８がネックになり，下段の単体表が最適解ではなくなってしまいます。
　逆に定数項を増大（ε をプラス側に増大）すると，最適解は直線ＰＳにそって移動し，Ｓ点を超えると青線に余裕ができてしまいます。このときの定数項は９６（ε＝２４）になります。
　この制約式の定数項のレンジは、下限６０（ε＝－１２）、上限９６（ε＝２４）であるといいます。

計算でレンジを求める

次に、上の結果から、定数項のレンジを求める方法を説明します。
　解説をあえて省略しますが，上の単体表の上段の表での制約式・スラック変数の部分の行列（黄）をＡとすると，下段のその部分（青）はＡの逆行列であるＡ^－１に相当します。そして，Ａ^－１に上段の列をＢとしてＡ^－１・Ｂの行列乗算を行うと，下段の対応する列になるのです。たとえばＢを上段の定数項（緑）とすると，下段の定数項Ｂ’（茶）は次のように計算できます。

　　　　　　　　　　　Ａ^－１　　　　　　Ｂ　　　　　　　　　　　　　　　　　Ｂ’
　　　┌　　 　　　　　 　　　　┐　┌　　┐　┌　　　　　　　　　 　┐　┌　　┐
　　　│　０.３３　－０.１７　０│×│７２│＝│ 0.33*72-0.17*48+0*48│＝│１６│
　　　│－０.３３　　０.６７　０│　│４８│　│-0.33*72+0.67*48+0*48│　│　８│　　①
　　　│　０.６７　－１.８３　１│　│４８│　│ 0.67*72-1.83*48+1*48│　│　８│
　　　└　　 　　　　　 　　　　┘　└　　┘　└　　　　　　　　　 　┘　└　　┘

定数項７２を（７２＋ε）とし、他はそのままとすると，先頭行は次のようになります。
　　　　０.３３Ｘ（７２＋ε）－０.１７Ｘ４８＋０Ｘ４８
　　　　＝１６＋０.３３ε
　ここで、定数項は負になれないので、１６＋０.３３ε≧０　→　ε≧－４８　となります。
　以下の行も同様に
　　　　　８－０.３３ε≧０　→　ε≦　２４
　　　　　８＋０.６７ε≧０　→　ε≧－１２
となります。
　この全体を満足する範囲（正での最小値、負での最大値）は
　　　ー１２≦ε≦２４　　　　定数項の下限＝７２－１２＝６０，上限＝７２＋２４＝９６
となり、グラフでの結果と一致します。

目的関数の値も次のようにして計算できます。

　　　┌　　 　　　　　 　　　┐　┌　　┐　┌　　┐
　　　│０.３３　－０.８３　０│×│７２│＝│６４│
　　　└　 　　　　　 　　　　┘　│４８│　└　　┘
　　　　　 　　　　　 　　　　　　│４８│
　　　　　 　　　　　 　　　　　　└　　┘
　　　０.３３×７２＋０.８３×４８＋０×４８＝６４
　ここで７２を７２＋ε とすると，目的関数の値は ６４＋０.３３ε となります。これはλ_１のレジューストコストが０.３３であること（赤）と一致します。

制約式　λ₂：２ｘ_１＋２ｘ_２≦４８ も基底にないので、次のように計算できます。
　　　１６－０.１７ε≧０　　→　ε≦　９６
　　　　８＋０.６７ε≧０　　→　ε≧－１２
　　　　８－１.８３ε≧０　　→　ε≦　　５
　　ー１２≦ε≦５４　　　　４８－１２＝３６（Ｙ軸），４８＋５＝５３（Ｔ点）
　

基底にある場合

制約式：１ｘ_１＋３ｘ_２≦４８ は基底にあります。定数項４８のうち、使ったのは８だけで、４０の余裕があります。
　現在でも余裕があるので、上限は∞になります。
　下限は、その余裕（８）を使い切ったときですから、ε≧－８　→　４８－８＝４０（Ｔ点）
　　すなわち、入力時の定数項（緑）－最適解の定数項（茶）になります。

価格（目的関数の係数）の変化とレンジ

現在はＰ点で商品の最適生産量が計算されていますが、極端に ｘ_１ の価格が高くなれば、現在の資源でできる限り ｘ_１ を生産し、その余りで ｘ_２ を生産するのが当然です。では、Ｐ点が最適となる ｘ_１ の価格の上下限はいくつかというのがここの問題です。

基底にある場合

ｘ_１を例にします。基底にあります。

グラフでの説明

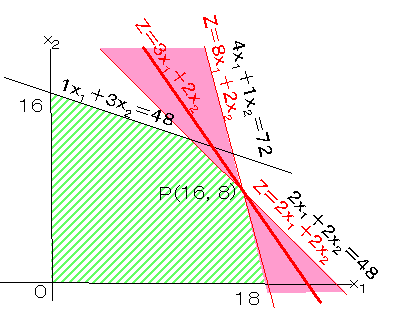
ｘ_１の価格をあげていくと，目的関数 ３ｘ_１＋２ｘ_２ の傾きは次第に垂直方向に変化していき，４ｘ_１＋１ｘ_２＝７２ と重なるようになります。そのときの目的関数のｘ_１の係数は８になります。逆に価格を下げていけば，２ｘ_１＋２ｘ_２≦４８ と重なりますが，そのときの係数の値は２になります。
　　　２≦ｘ_１価格≦８　　　－１≦ε≦５

計算でレンジを求める

ｘ_１の価格が ε だけ増加（－３-ε にした）とき，λ_１のシャドウ・プライス（赤）は0.333ε だけ増加して，0.333＋0.333ε になります。
これがマイナスになると，さらに最適解の計算をする必要がありますので，
　　0.333＋0.333ε≧０　→　ε≧－１
になります。
　λ_２についても同様に 　　0.833－0.17ε≧０　→　ε≦５
になります。 　λ_３では、係数が０なので、無視します。
　全体を満足する範囲は
　　　－１≦ε≦５　→　目的関数の下限＝－３－(－１)＝－２、上限＝-3－５＝－８
になります。
　この目的関数は、本来の価格を正負反転したのですから、
　　　　２≦ｘ₁の価格≦８
となります。

ｘ₂も基底にあるので、ｘ₁と同様にします。
ｘ_１の価格が ε だけ増加（－３-ε にした）とき，目的関数（赤）は、
　　λ₁：　0.333 - 0.333ε≧０　→　ε≦１
　　λ₂：　0.888 + 0.677ε≧０　→　ε≧-１.25
　　λ₂：　0/0　　　　　　　　　→　無視
　共通範囲：-１.25≦ε≦１　→　目的関数の下限＝-2-(-1.25)＝-0.75, 上限＝-2-1=-3
　　　　0.75≦ｘ₁の価格≦３
となります。

基底にない場合

この例では、このケースはありませんが、もし、そのような場合は、現在でも最適解は０（生産しない）のですから、価格の下限は－∞になります。上限は価格＋シャドウプライスになります。

理解度チェック

第１問

　目的関数
　　Ｚ＝４ｘ_１＋３ｘ_２　→最大
　制約条件
　　２ｘ_１＋１ｘ_２≦３０　　（ａ）
　　３ｘ_１＋４ｘ_２≦６０　　（ｂ）
　　１ｘ_１＋２ｘ_２≦２６　　（ｃ）

　

この解は次のようになります（グラフでは，ｘ_１をｘ，ｘ_２をｙとしています。

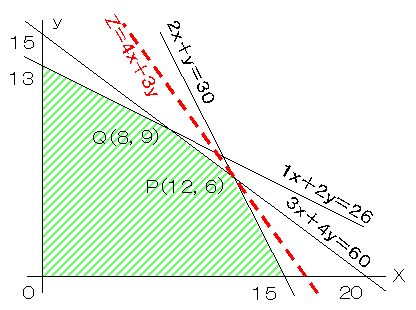
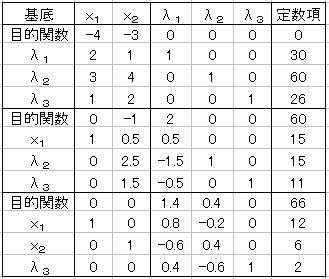
1. この３つの制約条件で余裕のある条件はどれか。 ☆
   「グラフが最適値Ｐを通らない」，「基底にλ_３がある」ことから，１ｘ_１＋２ｘ_２≦２６（ｃ）に余裕があることがわかる。
2. 制約条件：２ｘ_１＋１ｘ_２≦３０での３０が３０＋ε（ε は微小量）に増加すると，目的関数の値はどうなるか。 ☆
   最適解の表におけるλ_１のシャドウ・プライスが１.４ε であるから６６＋１.４ε になる。
3. 制約条件：２ｘ_１＋１ｘ_２≦３０＋εとしたとき、εを変化させても、すべての制約条件の結果（余裕がある、余裕がないの状態）が変化しない範囲を示せ。 ☆

   グラフから，最小値は２ｘ_１＋１ｘ_２が点Ｑ(８,９) を通るときである。このときの定数項は２×８＋１×９＝２５になる。また最大値は点(２０,０) を通るときで４０となる。
   シンプレックス法から求めるには，この定数項がε 増加したときは，最適解の表のλ_１の列から，次のような操作により，ε の範囲が－５≦ε≦１０であることがわかる。

   　　　変更前　　　εの変化　　　　εのとり得る範囲
   　　　１２　　　　０.８ε　　　　　－１５≦ε
   　　　　６　　　－０.６ε　　　　　　　　　ε≦１０
   　　　　２　　　　０.４ε　　　　　　－５≦ε

4. ここでは、ｘ_１の価格は４としたが，最適値が変化しない範囲でどの値までとることができるか。 ☆

   ４ｘ_１＋３ｘ_２のグラフは，この４が小さくなるにつれて傾きが水平に近づく。最適解が変わるのはこれが３ｘ_１＋４ｘ_２＝６０のグラフの傾きと一致したときであるから，そのときの４は３×３／４＝２.２５となる。逆に増加したときは２ｘ_１＋１ｘ_２と一致するときであるから，最大値は６となる。
   シンプレックス法から求めるには，最適解のｘ_１の行は，
   　　　１ｘ１＋０.８λ_１－０.２λ_２＝１２
   であり，ε 変化したときのλ１とλ２のシャドウ・プライスは次のようになる。

   　　　変更前　　　εの変化　　　　εのとり得る範囲　　　　４＋ε
   　　　１.４　　　　０.８ε　　　　－１.７５≦ε　　　　　４－１.７５＝２.２５
   　　　０.４　　　－０.２ε　　　　　　 　　　ε≦２　　　４＋２＝６