スタートページ> Web教材一覧> オペレーションズリサーチ> シミュレーション> シミュレーション(概要)
M/M/1型の待ち行列のポアソン到着・指数サービスに沿ったシミュレーションは、「M/M/1のシミュレーション」で示しました。しかし、そのモデルでは客到着間隔とサービス時間が0に近い確率が大きく、また、確率は小さいが非常に大きな値をとることがある特徴があります。
通常のシミュレーション対象の業務で、そのような極端な値を想定するのは実務的ではないし、極端な値が発生するとシミュレーション結果に大きな影響を与えるので、むしろ不適切な結果になります。
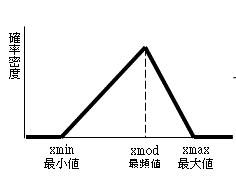
それでここでは、客到着間隔とサービス時間を、右図のような三角分布(参照:「分布に従う乱数の発生」)で与えることにしました。
また、初期状態が客がいないことにしているので安定状態になっておらず、統計結果に偏りが生じます。それを避けるために、最初の数人を統計の対象外にします。
すなわち、実際の到着客数は、「初期対象外客数+観測客数」になります。