予備知識:正規分布と標準偏差
この章では,統計に関する初歩の知識が必要になりますので,必要最小限の知識を簡単に学習しておきます(詳細は「確率・統計」シリーズ参照)。
正規分布
大勢の成年男子の身長の統計をとると,図のような釣鐘のような分布になります。このような分布を正規分布といいますが,多くの事象が正規分布になることが知られています。たとえば成年男子の身長は平均170cmで標準偏差が5cmであるというように,正規分布では,平均(μ:ミュー)と標準偏差(σ:シグマ)がパラメタになります。
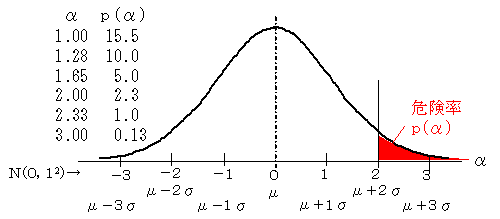
一般的には,個々の測定値xにα(アルファ)=(x-μ)/μの変換をすると,αは平均0,標準偏差1の正規分布になります。それをN(0,12)といいます。
図の赤い部分は,標準偏差がαよりも大きいときの確率pを示しています。図ではpを危険率としていますが,「成人男性の身長は180cmだ」としたときに,ある人の身長を測ったら180cm以上ある「危険」が2.3%というような意味で使っています。αとpの関係は図の表に掲げてあります。
統計では,一般に「ほんんど起こらない」レベル,すなわち危険率を5%とするのが通常です。厳しいときには1%を使います。すなわち,α=1.65あるいは2.33がよく用いられます。 (偏差値と3σ)
入試関係で「偏差値」という尺度がはやったときがありました。これは全国の受験生の成績をμ=50,σ=10に変換してN(50,102)としたことになります。偏差値70とはαが2のことです。偏差値70以上というとかなりの成績ですが,表で見るとその確率は2.3%,すなわち1000名のうち,上位23位以内にあることがわかります。
また,ちょっと変わった人を「あの人は3シグマだ」などということがありますが,1000人のうち1.3人の確率ですから,「よっぽど」変わった人だともいえますね。
標準偏差の加算
1日の出荷量にはバラツキがあります。その尺度が標準偏差です。1日の出荷量の標準偏差をσとしたとき,2日間の標準偏差を2σとしてもよいでしょうか? 1日目の出荷量と2日目の出荷量が互いに関係しないとすれば,両方が大きいほうになることもありますし,一方は大きいほうに,他方は小さいほうになって打ち消すこともあります。そのために2σは大きすぎることになります。
数学的なプロセス☆は省略しますが,L日間の標準偏差はσLではなくσ√Lになるのです。
1日の出荷量が,x=7~13の7つのケース(n=7)があるとします。1日の標準偏差σ1は次のようにして求められます。
観測点個数:n1=5
合計:S1=7+8+・・・+13=70
平均値:μ1=S1/n1=(7+8+・・・+13)/7
平均との差の平方和:T1=(7-10)2+(8-10)2+・・・+(7-10)2=16
分散:V1=T1/n1=16/7
標準偏差:σ1=√V=√16/7
出荷量x x-μ その平方
7 -3 9
8 -2 4
9 -1 1
10 0 0
11 1 1
12 2 4
13 3 9
-- --
合計 70 16
平均μ 10 分散=16/10 標準偏差=√16/10
これが2日間では,次のようになります。
合計:S2=2×S1=140
平均値:μ2=S2/n1=140/7=20=2×μ1
平均との差の平方和:T2=2×T2
分散:V2=T2/n1=2×16/7
標準偏差:σ2=√V2
=√2×16/7
=√2×σ1
すなわち,2日間の標準偏差は1日の標準偏差の√2倍になります。
安全在庫量
発注をしてから納入されるまでの期間Lを調達期間といいます。毎日の出荷量Dが一定ならば,在庫がD×Lになったら発注すればよいことになります。ところがL日間の間で,出荷にバラツキがあると,品切れが発生することになります。それを防ぐために,ある程度余計に在庫を持つ必要があります。それを安全在庫といいます。
極端なケースでは,世界中の人がいっせいに買いに来るかもしれません。それに備えるならば無限大に近い安全在庫を持つ必要がありますが,それはナンセンスでしょう。安全在庫を少なくすると,品切れの発生が多くなります。では,どの程度の安全在庫を持つべきかが問題になります。

1日の標準偏差をσとするとL日の標準偏差はσ√Lになりますが,ここで危険率を考慮して安全在庫量は次の式で与えます(危険率5%のときはα=1.65)。
安全在庫量の式
安全在庫量=ασ√L
これにより,発注点は次式になります。。
発注点の在庫量の式
発注点在庫量=調達期間内の平均出荷量+安全在庫量
=D×L+ασ√L
安全在庫は出荷が大きいほうにずれたときの品切防止を防ぐものでしたが,逆に小さいほうにずれるときには,入荷直後に在庫が大きくなってしまいます。そのずれる量は,危険率が同じにするならば,安全在庫量と同じですから,
最大在庫量の式
最大在庫量=発注量+2×安全余裕量
=Q+2ασ√L
となります。これは在庫倉庫に必要なスペースでもあります。
数値例
次のように記号をつけます。
Q:1回の発注量[300個]
D:1日の出荷量[5個/日]
σ:1日の出荷量の標準偏差[3個/日]
L:調達期間[16日]
α:=1.65(危険率5%)
安全在庫量=ασ√L=1.65×3×√16=19.8[個]
発注点=D×L+安全在庫量=5×16+19.8≒100[個]
最大在庫量=発注量+2×安全在庫量=300+2×19.8=340[個]